Page 235 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 235

8. ΤΥΠΟΣ ΣΥΝΑΡΤΗΣΗΣ (ΕΝΩΣΗ ΔΙΑΣΤΗΜΑΤΩΝ)
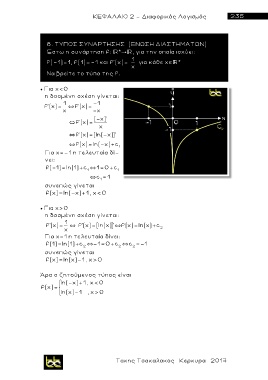
Έστω η συνάρτηση f: * , για την οποία ισχύει:
1
f(-1)=1, f(1)=-1 και f’ ( x)= x για κάθε χ *
Να βρείτε το τύπο της f.

 Για χ<0
η δοσμένη σχέση γίνεται:
1
f'(x)= ` f'(x)= -1
x -x
(-x)'
` f'(x)=

` f'(x)=[ln(-χ) ]'

` f(x)= ln(-χ) c 1
Για χ=-1 η τελευταία δί-
νει:
f(-1)= ln(1) c ` 1 0 c
1 1
` c = 1
1
συνεπώς γίνεται
f(x)=ln(-χ)+1 , χ<0

 Για χ>0
η δοσμένη σχέση γίνεται:
1
f'(x)= ` f'(x)=[ln(χ) ]' ` f(x)= ln(χ) c
x 2
Για χ=1 η τελευταία δίνει:
f(1)=ln(1) c ` -1 0 c ` c =-1
2 2 2
συνεπώς γίνεται
f(x)=ln(χ)-1 , χ>0

Άρ α ο ζητούμενος τύπος είναι
ln(-χ)+1 , χ< 0
f(x)=
ln(χ)-1 , χ> 0

Τακης Τσακαλακος Κερκυρα 2017