Page 237 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 237

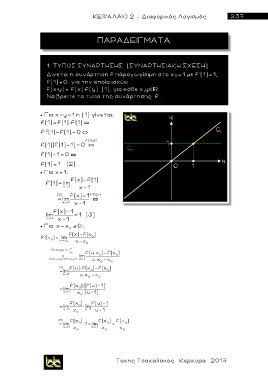
ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΤΥΠΟΣ ΣΥΝΑΡΤΗΣΗΣ (ΣΥΝΑΡΤΗΣΙΑΚΗ ΣΧΕΣΗ)
Δινεται η συνάρτηση f πάραγωγίσιμη στο χ 0 =1 με f'(1)=1,
f(1) 0, για την οποία ισχύει
f(x y)= f(x) f(y) (1), για κάθε χ,y
Να βρειτε το τυπο της συνάρτησης f .

 Για χ=y=1 η (1) γίνεται:
f(1)= f(1) f(1)

f (1)-f(1)= 0
2
f(1) 0
f(1)(f(1)-1)= 0

f(1)-1= 0
f(1)= 1 (2)

 Για χ=1:
f(x)-f(1)
f'(1)= lim
x 1 x-1
(2 ) f(x)-1 f'(1) = 1
= lim
x 1 x-1
f(x)-1
lim = 1 (3)
x 1 x-1

 Για x=x 0 0:
f(x)-f(x )
f '(x ) = lim 0 x-x 0 0
0
x
x
Θετουμε u = x
x 0 f(u× x )-f(x )
= lim 0 0
Αν x x 0 τοτε, u 1 u 1 u× x -x 0
0
(1) f(u)× f(x )-f(x )
=lim 0 0
u 1 u× x -x 0
0
f(x )×[f(u)-1]
=lim 0
u 1 x ×(u-1)
0
f(x ) f(u)-1
=lim 0 lim
u 1 x 0 u 1 u-1

(3) f(x ) f(x ) f(x )
= lim 0 1=lim 0 = 0
u 1 x 0 u 1 x 0 x 0

Τακης Τσακαλακος Κερκυρα 2017