Page 241 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 241

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΑΠΟΔΕΙΞΗ ΣΧΕΣΗΣ
Δίνεται η συνάρτηση f παραγωγίσιμη στο με f(0)=0, για
την οποία ισχύει: 2f'(x)=e x- f(x ) , για κάθε χ

Να αποδείξετε ότι f(x)-f(-x)=x, για κάθε χ .

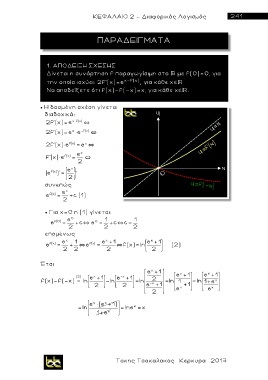
 Η δοσμένη σχέση γίνεται
διαδοχικά:
2f'(χ)= e x f (x )

2f'(χ)= e x e f (x )

2f'(χ) e f (x ) = e
x
e x
f'(χ) e f (x ) =
2
e x
(e f (x ) )' = '
2
συνεπώς
e x
e f (x ) = c (1)

2

 Για χ=0 η (1) γίνεται:
e 0 1 1
e f (0 ) = c ` e = c ` c=

0
2 2 2
επομένως
e x 1 e x 1 e +1
x
e f (x ) = ` e f (x ) = ` f(x)= ln (2)
2 2 2 2

Έτσι
e +1 x x
x
(2) e +1 e -x +1 e +1 e +1
x
f(χ)-f(-χ) = ln ln ln 2 ln 1 = ln 1+e x
2 2 e -x +1 x +1 x
2 e e

x
e x (e +1)
= ln = lne x χ
1+e x

Τακης Τσακαλακος Κερκυρα 2017