Page 244 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 244

4. ΑΠΟΔΕΙΞΗ ΣΧΕΣΗΣ
Δίνεται η συνάρτηση f: με f'(1)=3 και f(1)=1, για την
οποία ισχύει f''(2x-1)=12χ-6, για κάθε χ
Να αποδείξετε ότι
α) 2f(x)= χ +3χ-2, για κάθε χ
3

3
2
β) 2f(x-1) = χ -3χ +6χ-6, για κάθε χ

α )
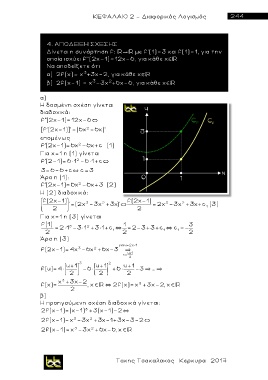
Η δοσμένη σχέση γίνεται
διαδοχικά:
f''(2x-1) = 12χ-6 `

[f'(2x-1) ]' =(6χ -6χ)'
2
επομένως
f'(2x-1) =6χ -6χ+c (1)
2
Για χ=1 η (1) γίνεται
f'(2-1) = 6 1 -6 1+c `
2

3 = 6-6 +c ` c 3
Άρα η (1):
f'(2x-1) =6χ -6χ+3 (2)
2
Η (2) διαδοχικά:

f(2x-1) ' =(2χ -3χ +3 )' ` f(2x-1) = 2χ -3χ +3 +c (3)
3
3
2
2
2 2 1
Για χ=1 η (3) γίνεται
1
f(1) =2 1 -3 1 +3 1+c ` =2-3+3+c ` c 3
3
2
2 1 2 1 1 2
Άρα η (3)
για u = 2x-1
f(2x-1) = 4χ -6χ +6 3 ~
2
3
x = u+1
2
u+1 3 u+1 2 u+1
f(u) = 4 -6 +6 3~... ~
2 2 2
3
χ +3χ-2
f(x) = , x ` 2f(x) = χ +3χ-2 , x
3
2
β )
Η προηγούμενη σχέση διαδοχικά γίνεται:
2f(x-1) =(χ-1) +3(χ-1)-2`
3
2f(x-1) = χ -3χ 2 3 1+3χ-3-2`
3
2f(x-1) = χ -3χ +6χ-6 , x
3
2

Τακης Τσακαλακος Κερκυρα 2017