Page 331 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 331

ΠΑΡΑΔΕΙΓΜΑΤΑ

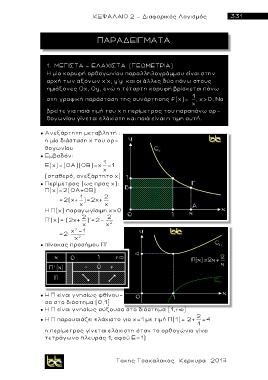
1. ΜΕΓΙΣΤΑ – ΕΛΑΧΙΣΤΑ (ΓΕΩΜΕΤΡΙΑ)
Η μία κορυφή ορθογωνίου παραλληλογράμμου είναι στην
αρχή των αξόνων χ'χ, y'y και οι άλλες δύο πάνω στους
ημιάξονες Οχ, Οy, ενώ η τέταρτη κορυφή βρίσκεται πάνω
1
στη γραφική παράσταση της συνάρτησης f(x)= , x>0. Nα
βρείτε για ποιά τιμή του χ η περίμετρος του παραπάνω ορ -

θογωνίου γίνεται ελάχιστη και ποιά είνα ι η τιμη αυτή.

● Ανεξάρτητη μεταβλητή :
η μία διάσταση χ του ορ-
θογωνίου
● Εμβαδόν:
1
Ε(χ)=(ΟΑ)(ΟΒ)=χ =1

(σταθερό, ανεξάρτητο χ)
● Περίμετρος (ως προς χ):
Π(χ)=2(ΟΑ+ΟΒ)
1 2
=2(χ+ )=2χ+
Η Π(χ) παραγωγίσιμη χ>0 με
2 2
Π'(χ)= (2χ+ )'=2-
2
2 1
=2×
2
● πίνακας προσήμου Π'

● Η Π είναι γνησίως φθίνου-
σα στο διάστημα (0,1]
● Η Π είναι γνησίως αύξουσα στο διάστημα [1,+þ]
2
● Η Π παρουσιάζει ελάχιστο για χ=1 με τιμή Π(1)= 2+ =4
1
η περίμετρος γίνεται ελάχιστη όταν το ορθογώνιο γίνει
τ ε τ ρ άγωνο πλευράς 1, αφού Ε=1)

Τακης Τσακαλακος Κερκυρα 2017