Page 334 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 334

4. OIKONOMIA (ΜΕΓΙΣΤΑ – ΕΛΑΧΙΣΤΑ)
To κόστος παραγωγής χ μονάδων ενός προιόντος μιάς βι-
ομηχανίας ημερησίως είναι
Κ(χ)=χ -12χ +3χ+5
3
2

Αν η τιμή του προιόντος είναι Τ(χ)=38-4χ ανά μονάδα, να
βρείτε την ημερήσια παραγωγή, ώστε η βιομηχανία να έχει
το μέγιστο δυνατό κέρδος.

Έστω

● Ρ(χ) το κέρδος

● Ε(χ) τα ημερήσια εσοδα
Έτσι για χ > 0

● Ε(χ)=χ Τ(χ)=χ(38-4χ)

=38χ-4 χ 2
και

Ρ(χ)=Ε(χ)-Κ(χ)

= 38χ-4χ -(χ -
3
2

-12χ +3χ+5)
2
= 38χ-4χ -χ +12χ -
2
2
3

-3 χ -5

= -χ +8χ +35χ-5
2
3
που είναι παραγωγίσιμη για χ>0 με

Ρ'(χ)= (-χ +8χ +35χ-5)' = -3χ +16χ35
2
3
2

5 0, απορρίπτεται
● Ρ'(χ)=0`...` 3
χ= 7> 0, δεκτή

Ρ'(χ)>0` χ<7

Ρ'(χ)<0` χ>7

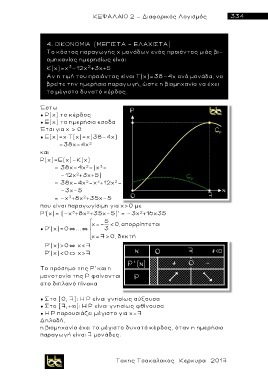
To π ρ όσημο της Ρ' και η

μονοτονία της Ρ φαίνονται

σ τ ο διπλανό πίνακα

● Στο [0, 7]: Η Ρ είναι γνησίως αύξουσα

● Στο [7,+þ): Η Ρ είναι γνησίως φθίνουσα
● Η Ρ παρουσιάζει μέγιστο για x=7

Δηλαδή,

η βιομηχανία έχει το μέγιστο δυνατό κέρδος, όταν η ημερήσια
παραγωγή είναι 7 μονάδες.

Τακης Τσακαλακος Κερκυρα 2017