Page 74 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 74

ΣΥΝΑΡΤΗΣΗ σφχ
Έστω η συνάρτηση
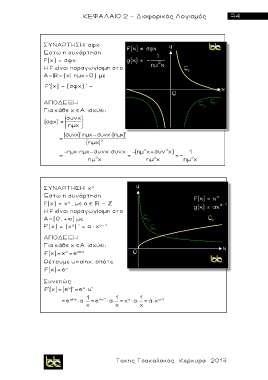
f(x) = σφχ.
Η f είναι παραγωγίσιμη στο
Α= -{χ| ημχ=0} με

f’ ( x) = (σφχ) ’ = - 1 2
ημ χ
ΑΠΟΔΕΙΞΗ
Για κάθε x Α ισχύει:
συνχ
( x )' ημx '

( )'× ×( )'
(ημx ) 2
× συνχ× συν ( 2 συν χ) 1
2
ημ x ημ x ημ x
2
2
2

Σ Υ Ν ΑΡΤΗΣΗ χ
α
Έστω η συνάρτηση
f(x) = χ , με α - ¢
α
Η f είναι παραγωγίσιμη στο
Α=(0, +þ) με
f’ ( x) = ( χ α ) ’ = α × χ α - 1

ΑΠΟΔΕΙΞΗ
Για κάθε x Α ισχύει:

α
f(x)=x =e αlnx

Θέτουμε u=αlnx, οπότε
f(x)=e
u

Συνεπώς e × u'
u
u
f'(x)=(e )'
e lnx × × 1 e lnx × × 1 = x × × 1 = × x 1

Τακης Τσακαλακος Κερκυρα 2017