Page 75 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 75

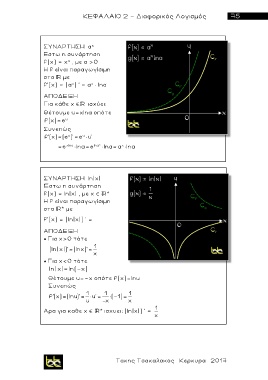
Σ Υ Ν ΑΡΤΗΣΗ α
χ
Εστω η συνάρτηση
f(x) = χ , με α >0
α
Η f είναι παραγωγίσιμη
στο μ ε
f’ ( x) = ( α χ ) ’ = α × lna
χ

ΑΠΟΔΕΙΞΗ
Για κάθε x ισχύει: f(x)= e ln
Θέτουμε u=xlnα οπότε
f(x)=e
u
Συνεπώς
f'(x)=(e )' e × u'
u
u
e ln × ln e ln × ln = × ln

Σ Υ Ν ΑΡΤΗΣΗ ln|x|
Έστω η συνάρτηση

f(x) = ln|χ| , με x *

Η f είναι παραγωγίσιμη
στο * με
f’ ( x) = (ln|x|) ’ = 1

χ
ΑΠΟΔΕΙΞΗ
 Για χ>0 τότε 1

(ln| x|)' =(lnx)' = x
 Για χ<0 τότε
ln|x|=ln(-x)

Θέτουμε u=-x οπότε f(x)=lnu
Συνεπώς

f'(x) (lnu)' 1 × u' = 1 ×(-1)= 1
u x x
1
Αρα για καθε x * ισχυει: (ln|x|) ’ = χ

Τακης Τσακαλακος Κερκυρα 2017