Page 77 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 77

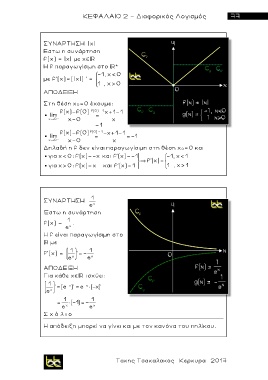
Σ Υ Ν ΑΡΤΗΣΗ |χ|
Εστω η συνάρτηση
f(x) = |χ| με χ
Η f παραγωγίσιμη στο *
με f’ ( x)=(|χ | ) ’ = -1, χ< 0
1 , χ> 0

ΑΠΟΔΕΙΞΗ

Στη θέση χ 0=0 έχουμε:
lim f(x)-f(0) f(0) 1 x+1-1
x 0 x-0 x
1
lim f(x)-f(0) f(0) 1 -x+1-1 1
x 0 x-0 x
Δηλαδή η f δεν είναι παραγωγίσιμη στη θέση χ 0=0 και
για χ< 0: f(x)=-χ και f'(x)=-1 -1, χ< 1
για χ> 0: f(x)= χ και f'(x)= 1 f'(x)= 1 , χ> 1

Σ Υ Ν ΑΡΤΗΣΗ 1
e
Έστω η συνάρτηση

f(x) = 1 .
e
Η f είναι παραγωγίσιμη στο
μ ε
f’ ( x) = 1 ' =- 1
e χ e χ

ΑΠΟΔΕΙΞΗ
Για κάθε x ισχύει:
1 ' =(e )' = e ×( )'
e
1 ×( 1) 1
e e
Σ χ ό λ ι ο

Η απόδειξη μπορεί να γίνει και με τον κανόνα του πηλίκου.

Τακης Τσακαλακος Κερκυρα 2017