Page 82 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 82

στ)
Α s =

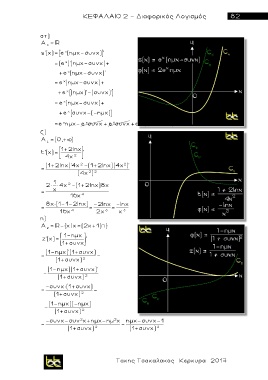
s'(x)= e (ημx-συνx) '
x
=(e )'(ημx-συνx)+
x
+e (ημx-συνx)'
x
x
= e (ημx-συνx)+
+e x (ημx)'-(συνx)'

x
= e (ημx-συνx)+
+e x συνx-(-ημx)

= e ημx- e συνx + e συνx +e ημx = 2e ημx
x
x
x
x
x
ζ )
Α =(0,+ )
t
1+2lnx
t'(x)= '
4x 2
(1+2lnx)'4x -(1+2lnx)(4x )'
2
2
=
(4x )
2 2
2× 1 × 4x -(1+2lnx)8x
2
= x
16x 4
8x×(1-1-2lnx) - 2lnx - lnx
= = =
16x 4 2x 3 x 3
η)
Α = {x| x (2κ+1)π}
z
1-ημx
z'(x)= '
1+συνχ

(1-ημx)'(1+συνχ)
=
(1+συνχ) 2

(1-ημx)(1+συνχ)'
-
(1+συνχ) 2
-συνx×(1+συνχ)
=
(1+συνχ) 2

(1-ημx)(-ημχ)
-
(1+συνχ) 2

-συνx-συν x+ημx-ημ χ ημx-συνx-1
2
2
= =
(1+συνχ) 2 (1+συνχ) 2

Τακης Τσακαλακος Κερκυρα 2017