Page 83 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 83

2.
Να βρείτε τη παράγωγο των συναρτήσεων:
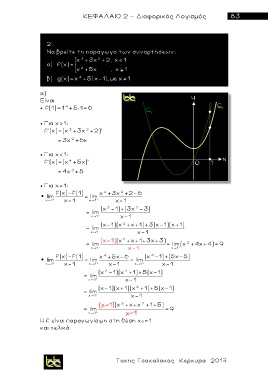
x 3 +3x 2 +2, x< 1
α) f(x)=
x 4 +5x , x 1
4
β) g(x)=x +5|x-1|, με x 1

α )

Είναι
 f(1)=1 +5× 1=6
4

 Για χ>1:
f '(x)=(x 3 +3x 2 +2)'

= 3x 2 +6x

 Για χ<1:

f '(x)=(x +5x)'
4

= 4x 3 +5

 Για χ=1:
f(x)-f(1) 3 2
lim = lim x +3x +2-6
x 1 - x-1 x 1 - x-1
3
(x -1)+(3x -3)
2
= lim - x-1

1
x

= lim (x-1)(x 2 +x+1)+3(x-1)(x+1)
x 1 - x-1
2
= lim (x-1) (x +x+1+3x+3) = lim(x 2 +4x+4)= 9
-
x 1 - x 1 x 1 -
f(x)-f(1) x 4 +5x-6 (x -1)+(5x-5)
4
lim = lim = lim
x 1 + x-1 x 1 + x-1 x 1 + x-1
(x -1)(x 2 +1)+5(x-1)
2
= lim +
x 1 x-1
= lim (x-1)(x+1)(x 2 +1)+5(x-1)
x 1 + x-1
1
(x - )(x 3 +x+x 2 +1+5)
= lim 9
x 1 + x-1

Η f είναι παραγωγίσιμη στη θέση χ 0=1
και τελικά

Τακης Τσακαλακος Κερκυρα 2017