Page 86 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 86

ΠΑΡΑΔΕΙΓΜΑΤΑ

1.
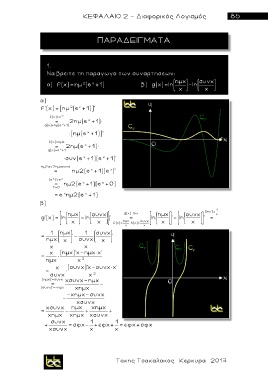
Να βρειτε τη παραγωγο των συναρτησεων:
ημx συνx
2
x
α) f(x)=ημ (e +1) β) g(x)= ln x -ln x

α )

f '(x) =[ημ (e +1)]'
x
2
=
x
f(x) = x 2 2ημ(e +1)
x
g(x) = ημ(e + 1)

[ημ(e +1)]'
x
f(x) = ημx
= 2ημ(e +1)
x
x
g(x) = e + 1

συν(e +1)(e +1)'
x
x

ημ2α = 2ημασυνα
= ημ2(e +1)(e )'
x
x
(e )' = e x
x
= ημ2(e +1)(e +0)
x
x
1' = 0
= e ημ2(e +1)
x
x

β)
1
ημx συνx g(x) = lnx ημx συνx ( lnx)' =
x
g'(x) = ln -ln ' = ln '- ln ' =
x x f(x) = ημx , h(x) = συνx x x
x
x
= 1 ημx '- 1 συνx '
ημx x συνx x
x x
x (ημx)'x-ημx× x'
= ημx x 2

- x × (συνx)'x-συνx× x'
συνx x 2

( ημx)' = συνx xσυνx-ημx
=
( συνx)' = - ημx xημx -
-xημx-συνx
-
xσυνx
= xσυνx - ημx + xημx +
xημx xημx xσυνx
1
1
συνx
+ xσυνx = σφx- x +εφx+ x = εφx+σφx

Τακης Τσακαλακος Κερκυρα 2017