Page 91 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 91

3.
α χ
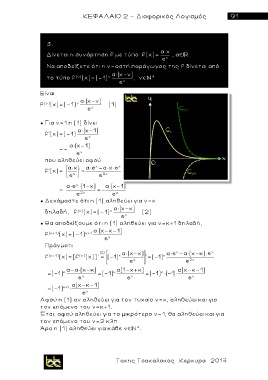
Δίνεται η συνάρτηση f με τύπο f(x)= e x , α .
Να αποδ ε ίξετε ότι η ν-ο σ τ ή παράγωγος της f δίνεται από
α (χ-ν)
το τύπ ο f ( ν ) (x)=(-1) ν e x , ν ©*

Eίναι
α (χ-ν)
f ( ν ) (x)=(-1) ν (1)
e x

● Για ν=1 η (1) δίνει
α (χ-1)
f'(x)=(-1)
e x
α (χ-1)
=-
e x
που αληθεύει αφού
α χ α e x α χ e x
f'(x)= '
e x e 2x

α e x (1 χ) α ( 1)
=
e 2x e x
● Δεχόμαστε ότι η (1) αληθεύει για ν=κ
α (χ-κ)
δηλαδή, f ( κ ) (x)=(-1) κ (2)
e x
● Θα α π οδείξουμε ότι η (1) αληθεύει για ν=κ+1 δηλαδή,
α (χ-κ-1)
f ( κ + 1 ) (x)=(-1) κ + 1
e x
Π ρ άγματι
x
(2 ) α×(χ-κ) α× e -α×(χ-κ) e x
f ( κ + 1 ) (x)=[f ( κ ) (x)]' (-1) κ ' (-1) κ
e x e 2x
α-α×(χ-κ) α(1-χ+κ) α(χ-κ-1)
(-1) κ (-1) κ (-1) κ ( 1 )
e x e x e x
α(χ-κ-1)
(-1) κ+1
e x
Αφού η (1) αν αληθεύει για τον τυχαίο ν=κ, αληθεύει και για
τον επόμενο του ν=κ+1.
Έτσι, αφού αληθεύει για το μικρότερο ν=1, θα αληθεύει και για
τον επόμενο του ν=2 κλπ
Άρα η (1) αληθεύει για κάθε ν ©*.

Τακης Τσακαλακος Κερκυρα 2017