Page 95 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 95

4
g(x ) =g(4)=4+ln(4-3) =4+ln1=
2
0
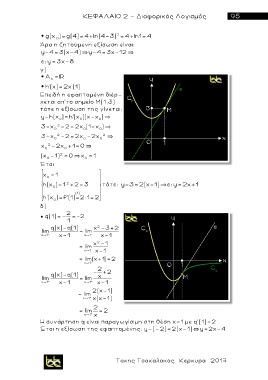
Άρα η ζητούμενη εξίσωση είναι:
y-4=3(x-4) y-4=3x-12

ε: y= 3x-8
γ )
A =
h
h'(x)=2x (1)
Επειδή η εφαπτομένη διέρ-
χεται απ'το σημείο Μ(1,3)
τότε η εξίσωση της γίνεται:
y-h(x )= h'(x )(x-x )
0
0
0
3-x 2 -2= 2x (1-x )
0 0 0
3-x 0 2 -2= 2x -2x 0 2
0
x 2 -2x +1= 0
0 0
2
(x -1) = 0 x = 1
0
0
Έτσι
x = 1
0
h(x )= 1 2 +2= 3 τότε: y-3=2(x-1) ε:y=2x+1
0
(1)
h'(x )= f'(1)=2× 1= 2
0
δ )
2
● q(1)= - 2
1
q(x)-q(1) χ -3+2
2
lim = lim
x 1 x-1 x 1 x-1
χ -1
2
= lim
x 1 x-1
= lim(χ+1) 2
x 1
- 2 +2
q(x)-q(1) χ
lim = lim
x 1 x-1 x 1 x-1
2(χ-1)
= lim
x 1 x(x-1)
2
= lim = 2
x 1 x
Η συνάρτηση q είναι παραγωγίσιμη στη θέση χ=1 με q'(1)=2
Έτσι η εξίσωση της εφαπτομένης: y-(-2)=2(x-1)`y=2x-4

Τακης Τσακαλακος Κερκυρα 2017