Page 87 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 87

2.
Να βρείτε τη παράγωγο των συναρτήσεων:
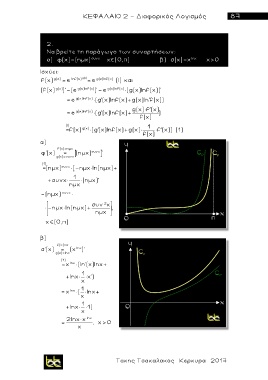
α) φ(x)=(ημx) συνx χ (0,π) β) σ(x)= x lnx χ>0

Ισχύει:

f(x) g(x) = e lnf(x) g(x) = e g(x)lnf(x) (I) και
(f(x) g(x) )' =(e g(x)lnf(x) )' = e g(x)lnf(x) ×( g(x)lnf(x))'

= e g(x)lnf(x) ×( g'(x)lnf(x)+g(x)ln'f(x))

g(x)× f'(x)
= e g(x)lnf(x) ×( g'(x)lnf(x)+ f(x) )

(I) 1
=f(x) g(x) ×( g'(x)lnf(x)+g(x)× × f'(x)) (1)
f(x)
α )
f(x) = ημx
φ'(x) = (ημx) συνx '
g(x) = συνx
(1)
=(ημx) συνx ×[- ημx× ln(ημx)+

+συνx× 1 ×(ημx)'
ημx

=(ημx) συνx ×

2

× - ημx× ln(ημx)+ συν x ,
ημx

x (0,π)

β)

f(x) = x
σ'(x) = (x lnx )'
g(x) = lnx
(1)

=x lnx ×( ln'(x)lnx+

+lnx× 1 × x')
x
1
= x lnx ×( × lnx+
x
+lnx× 1 × 1)
x

= 2lnx× x lnx , x 0
x

Τακης Τσακαλακος Κερκυρα 2017