Page 78 - diaforikos

ΚΕΦΑΛΑΙΟ 2 - Διαφορικός Λογισμός 78

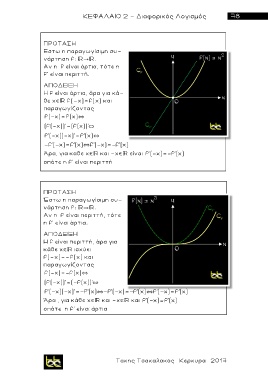
ΠΡΟΤΑΣΗ
Εστω η παραγωγίσιμη συ-
νάρτηση f: .

Αν η f είναι άρτια, τότε η
f’ είναι περιττή.
ΑΠΟΔΕΙΞΗ
Η f είναι άρτια, άρα για κά-
θε χ f(-x)=f(x) και

παραγωγίζοντας
f(-x)= f(χ) `
(f(-x))' =(f(χ))'`
f'(-x)(-χ)' = f'(χ) `

-f'(-x)=f'(χ) ` f'(-x)=-f'(χ)
Άρα, για καθε χ και -χ είναι f'(-x)=-f'(χ)
οπότε η f' είναι περιττή

ΠΡΟΤΑΣΗ
Έστω η παραγωγίσιμη συ-
νάρτηση f: .
Αν η f είναι περιττή, τότε

η f’ είναι άρτια.

ΑΠΟΔΕΙΞΗ
Η f είναι περιττή, άρα για
κάθε χ ισχύει

f(-x)=-f(x) και
παραγωγίζοντας
f(-x)=-f(χ) `

(f(-x))' =(-f(χ))'`
f'(-x)(-χ)' =-f'(χ) ` -f'(-x)=-f'(χ) ` f'(-x)=f'(χ)
Άρα , για κάθε χ και -χ και f'(-x)=f'(χ)
οπότε η f' είναι άρτια

Τακης Τσακαλακος Κερκυρα 2017