Page 103 - olokliroma

103
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

2. ΑΡΡΗΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
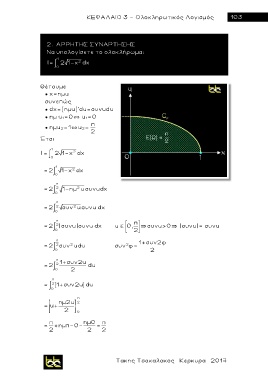
Να υπολογίσετε το ολοκλήρωμα:
1
2
Ι= 0 2 1 χ dx

Θέτουμε
● χ = ημu
συνεπώς
● dx=(η μ u)'du=συνudu

● ημ u 1=0` u 1=0
● ημu 2=1`u 2=
2

Έτσι

1
Ι = 2 1-χ dx
2
0
1
= 2 1-χ dx
2
0

π
2
= 2 2 1-ημ u συνudx
0
π
2
= 2 2 συν u συνu dx
0
π π
= 2 2 | συνu| συνu dx u 0, ~συνu>0~ |συνu|= συνu
0 2

π 1+συν2φ
2
2
= 2 2 συν u du συν φ=
0 2
π 1+συν2u
= 2 2 du
0 2

π
= 2 (1+συν2u ) du
0

π
ημ2u 2
= u+
2 0

π ημ0 π
= +ημπ-0- =
2 2 2

Τακης Τσακαλακος Κερκυρα 2017