Page 105 - olokliroma

105
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΚΛΑΔΙΚΗΣ ΣΥΝΑΡΤΗΣΗΣ
x -3x+2
2
Δίνεται η συνάρτηση f με τύπο f(x)= x-1 , x< 1
2x-3 , x 1

Να υπολογίσετε το ολοκλήρωμα:
Ι= 2 f(x) dx
0

H f έχει πεδίο ορισμού
Α=

η f είναι συνεχής στο
● (- , 1) σαν ρητή
● (1, + ) σαν πολυωνυμική
● Στο x 0 =1 είναι

2
lim f(x)= lim x -3x+2
x 1 - x 1 - x-1
(x-1)(χ-2)
= lim
x 1 - x-1
= lim(χ-2)=-1
x 1 -
lim f(x)= lim(2χ-3) =-1
x 1 + x 1 +
● f(1)=-1
συνεπώς, lim f(x)= lim f(x)=f(1)
x 1 - x 1 +
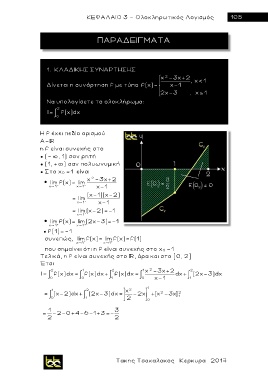
που σημαίνει ότι η f είναι συνεχής στο x 0 =1
Τελικά, η f είναι συνεχής στο , άρα και στο [0, 2]
Έτσι
2
2 1 2 1 x -3x+2 2
Ι= f(x) dx f(x) dx f(x) dx dx (2x-3) dx
0 0 1 0 x-1 1

1 2 χ 2 1
2
(x-2) dx (2x-3) dx -2χ [χ 2 3 ]
0 1 2 0 1
1 3
-2-0 4 6 1 3 -
2 2

Τακης Τσακαλακος Κερκυρα 2017