Page 110 - olokliroma

110
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΑΝΑΓΩΓΙΚΟΣ ΤΥΠΟΣ
2
v
Αν Ι ν= 1 x (lnx) dx , ν ©*
● Να αποδείξετε ότι 2Ι ν+νΙ ν - 1 = 4(ln2) , ν 2
ν
● Να υπολογίσετε τα ολοκληρώματα Ι 1+Ι 2, Ι 1, Ι 2

Έχουμε
2 2
● 2Ι +vΙ 2 χ(lnχ) dx+v χ(lnχ) v 1 dx
v
ν-1
ν
1 1
2 2 (lnχ) v
= 2 χ(lnχ) dx+v χ 2 ' dx
v
1 1 v
2 (lnχ) v 2 2 (lnχ) v
= 2 χ(lnχ) dx+v χ 2 -v (χ )' dx
v
2
1 v 1 v
1
2 2
v
v
v 2
= 2χ (lnχ) dx +[χ 2 (lnχ) ] - 2χ ( lnχ) dx
1 1 1
= 4×(ln2) v

2
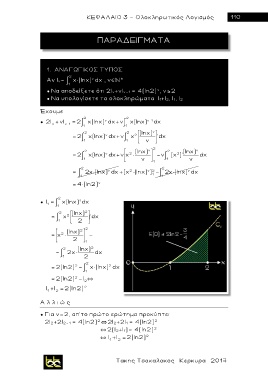
● Ι χ(lnχ) dx
1
1
1
2 (lnχ) 2
= χ 2 ' dx
1 2
(lnχ) 2 2
= χ 2 -
2 1
- 2 2χ (lnχ) 2 dx
1 2
2
2
2
= 2(ln2) - χ (lnχ) dx
1
= 2(ln2) -Ι `
2
2
Ι Ι 2(ln2) 2
1
2

Α λ λ ι ώ ς
● Για ν=2, απ'το πρώτο ερώτημα προκύπ τει
2 Ι 2+2Ι 2 - 1 = 4(ln2) `2Ι 2+2Ι 1 = 4(ln2)
2
2
`2(Ι 2+ Ι 1)= 4(ln2) 2
` Ι Ι 2(ln2)
2
1 2

Τακης Τσακαλακος Κερκυρα 2017