Page 98 - olokliroma

98
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

3. ΡΗΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
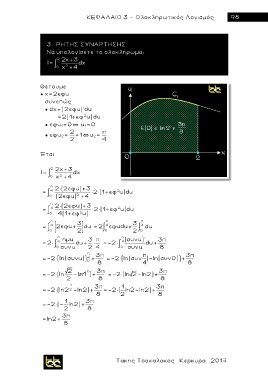
Να υπολογίσετε το ολοκλήρωμα:
2 2 3
Ι= 0 χ 2 4 dx

Θέτουμε
● x=2εφu
συνεπώς
● dx=(2εφu)'du
=2(1+εφ u)du
2
● ε φ u 1=0` u 1=0
2
● ε φ u 2= =1`u 2=
2 4

Έτσι

2 2χ+3
Ι= dx
0 χ +4
2
π 2 (2εφu)+3
= 4 2 (1+εφ u)du
2
2
0 (2εφu) +4
π 2 (2εφu)+3
= 4 2 (1+εφ u)du
2
2
0 4(1+εφ u)
π 3 π 3 π
= 4 2εφu+ du = 2 4 εφudu 4 du
0 2 0 2 0
π ημu 3 π π (συνu)' 3π
= 2 4 du =-2 4 du
0 συνu 2 4 0 συνu 8

π 3π π 3π
=-2 [ln| συνu|] 4 =-2 [ln(συν )-ln(συν0)]
0 8 4 8
0
=-2 (ln 2 - ln1 ) 3π =-2 (ln 2-ln2) 3π
2 8 8
1 3π 1 3π
=-2 (ln2 -ln2) =-2 ( ln2-ln2)
2
8 2 8
1 3π
=-2 (- ln2)
2 8

= ln2+ 3π
8

Τακης Τσακαλακος Κερκυρα 2017