Page 96 - olokliroma

96
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

ΠΑΡΑΔΕΙΓΜΑΤΑ

1. ΡΗΤΗΣ ΣΥΝΑΡΤΗΣΗΣ
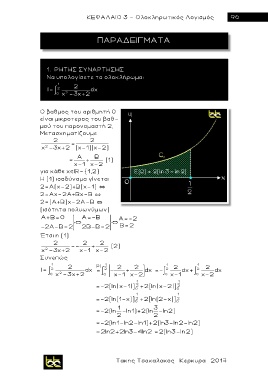
Να υπολογίσετε το ολοκλήρωμα:
1 2

Ι= 0 χ 2 dx
2
3 2

Ο βαθμος του αριθμητή 0
είναι μικροτερος του βαθ-
μού του παρονομαστή 2,
Μετασχηματίζουμ ε
2 2
χ 2 3 2 (χ-1)(χ-2)

(1)
χ-1 χ-2
για κάθε χ -{1,2}

Η (1) ισοδύναμα γίνεται
2=Α(χ-2)+Β(χ-1) `
2=Αχ-2Α+Βχ-Β `
2=(Α+Β)χ-2Α-Β `
(ισότητα πολυωνύμων)
Α+Β=0 Α=- Β Α=- 2
` `
-2Α-Β=2 2Β-Β=2 Β=2
Έτσι η (1)
2 2 2 (2)
χ 2 3 2 χ-1 χ-2
Συνεπώς

1 2 (2) 1 2 2 1 2 1 2
Ι= 2 dx 2 dx 2 dx 2 dx
2
0 χ -3χ+2 0 χ-1 χ-2 0 χ-1 0 χ-2
1 1
=-2[ln| x-1|] 2 2[ln| x-2|]
2
0 0
1 1
=-2[ln(1-x)] 0 2 2[ln(2-x)]
2
0
1 3
=-2(ln ln 1) 2(ln -ln 2)
2 2
=-2(ln 1 ln2 ln 1) 2(ln3-ln 2-ln 2)

=2ln2 2ln3-4ln 2 =2(ln3-ln 2)

Τακης Τσακαλακος Κερκυρα 2017