Page 260 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 260

Επομένως,
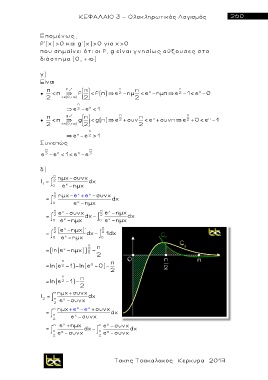
f'(x)>0 και g'(x)>0 για χ>0
που σημαίνει ότι οι f, g είναι γνησίως αύξουσες στο
διάστημα (0, + )

γ )
Είναι
f π π π π
π
π
● ~ f < f(π)~e -ημ < e -ημπ~e -1< e -0
2
2
2 x (0, + ) 2 2
π
~ e -e < 1
π
2
g π π π π
● ~ g < g(π)~e +συν < e +συνπ~e +0< e -1
π
π
2
2
2 x (0, + ) 2 2
π
π
~ e -e > 1
2
Συνεπώς
π π
e -e < 1< e -e
π
π
2
2

δ )
π ημχ-συνχ
I = 2 dx
1
x
0 e -ημχ
π ημχ-e +e x -συνχ
x
= 2 dx
x
0 e -ημχ
π e -συνχ π e -ημχ
x
x
= 2 dx 2 dx
x
x
0 e -ημχ 0 e -ημχ
π (e -ημχ)' π
x
= 2 dx 2 1 dx
x
0 e -ημχ 0
π π

=[ln(e -ημχ)] 2
x
0 2
π π
=ln(e -1)-ln(e -0)
0
2
2
π π
=ln(e -1)
2
2
π ημχ+συνχ
I dx
2 π e -συνχ
x
2
x
π ημχ+e -e x +συνχ
= dx
π e -συνχ
x
2
x
x
π e +ημχ π e -συνχ
= dx dx
π e -συνχ π e -συνχ
x
x
2 2
Τακης Τσακαλακος Κερκυρα 2017