Page 261 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 261

x
π (e -συνχ)' π
= dx 1 dx
π e -συνχ π
x
2 2
π
=[ln(e -συνχ)] π
x
π 2
2
π π
=ln(e +1)-ln(e -1)
2
2
Έτσι
π π π π
Ι =Ι 1-Ι 2= ln(e -1) -ln(e +1)+ln(e -1)
2
2
2 2
π
π π (e -1) 2
2
2ln(e -1)-ln(e +1) ln(e -1) -ln(e +1)= ln
2
π
π
2
2
e +1
π

ε )
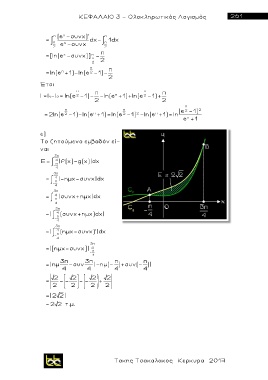
Το ζητούμενο εμβαδόν εί-
ναι
3π
Ε = 4 | f(x) g(x)| dx
π
4
3π
= 4 |-ημχ-συνx| dx
- π
4
3π
= 4 | συνχ+ημx| dx
- π
4
3π
=| 4 (συνχ+ημx) dx|
- π
4
3π
=| 4 (ημχ-συνχ)' | dx
- π
4
3π

=|[ημχ-συνx]| 4
- π
4
3π 3π π π
=| ημ -συν |-ημ( - )+συν( - )|
4 4 4 4
2 2 2 2
= - - - - +
2 2 2 2

=| 2 2|
= 2 2 τ.μ.

Τακης Τσακαλακος Κερκυρα 2017