Page 262 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 262

15. ΕΠΙΛΟΓΗ
Δίνονται οι συναρτήσεις f, g με τύπο
1
f(x)=x+lnx-ln(x+1) και g(x)=x+

α) Να μελετήσετε τις f, g ως προς τη μονοτονία και να
βρείτε τα όρια lim f(x), lim g(x)
x +
x +
β ) Να βρείτε το σύνολο τιμών της f και το πλήθος των ρι-
ζών της εξίσωσης f(x)=0
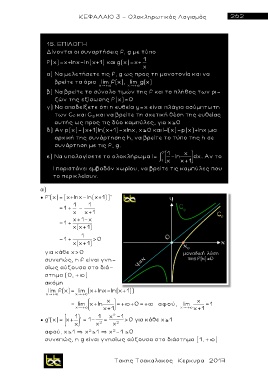
γ ) Να αποδείξετε ότι η ευθεία y=x είναι πλάγια ασύμπτωτη

των C f και C g και να βρείτε τη σχετική θέση της ευθείας
αυτής ως προς τις δύο καμπύλες, για χ 0
δ) Αν p(x)=(x+1)ln(x+1)-xlnx, x 0 και Η(χ)=p(x)+lnx μια
αρχική της συνάρτησης h, να βρείτε το τύπο της h σε
συνάρτηση με τις f, g.
ε) Να υπολογίσετε το ολοκλήρωμα Ι= 2 1 -ln x dx. Αν το
1 x x+1
Ι παριστάνει εμβαδόν χωρίου, να βρείτε τις καμπύλες που
το περικλείουν.

α)
● f'(x)=[x+lnx-ln(x+1)]'
1 1
=1 + -
1
χ+1-χ
=1 +
χ(χ+1)
1
=1 + >0
χ(χ+1)

για κάθε χ>0
συνεπώς, η f είναι γνη-
σίως αύξουσα στο διά-
στημα (0, + )
ακόμη

lim f(x)= lim (x+lnx-ln(χ+1))
x + x +
x x
= lim x+ln 0 αφού, lim 1
x + 1 x + 1

1 1 χ 2 1
● g'(x)= x ' = 1 = >0 για κάθε χ 1
χ 2 χ 2
αφού, χ 1 ~ χ 2 1 ~ χ -1 0
2
συνεπώς, η g είναι γνησίως αύξουσα στο διάστημα [1, + )

Τακης Τσακαλακος Κερκυρα 2017