Page 264 - olokliroma

ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός 264

x
f(x)-x= x+lnx-ln(χ+1)-x=lnx-ln(x+1)= ln <0
χ+1
x
αφού 0<χ<χ+1~ 0 <1
χ+1
επομένως, η ασύμπτωτη y=x είναι "πάνω" από τη C f.
● Για χ 1
1 1
g(x)-x= x+ -x= >0 (χ 1>0)
x x
επομένως, η ασύμπτωτη y=x είναι "κάτω" από τη C g.

δ)
Αφού η Η είναι μια αρχική της h τότε
h(x)=H'(x)
=p'(x)+(lnx)'
=[(x+1)ln(x+1)]'-(xlnx)'+(lnx)'
=(x+1)'ln(x+1)+(x+1)[ln(x+1)]'-(x)'lnx-x(lnx)'+(lnx)'
x+1 1 1
= ln(x+1)+ -lnx-x
x+1 x x
1
= ln(x+1)+1-lnx-1
x
1
= ln(x+1) +x-x-lnx
x
1
= x -(x+lnx-ln(x+1))
x

=g(x)-f(x)

ε)
● p(1)=2ln2-1ln1=2ln2
● p(2)=3ln3-2ln2

2 1 x
I= -ln dx
1 x x+1
( ) 2
(g(x)-f(x)) dx
1
2
h(x) dx
1
=H(2)-H(1)
=p(2)+ln2-p(1)-ln1

=3ln3-2ln2+ln2-2ln2-0
=3ln3-3ln2=3(ln3-ln2)
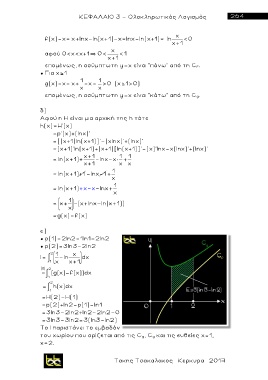
Το Ι παριστάνει το εμβαδόν
του χωρίου που ορίζεται από τις C g, C g και τις ευθείες χ=1,
χ=2.

Τακης Τσακαλακος Κερκυρα 2017