Page 36 - olokliroma

36
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

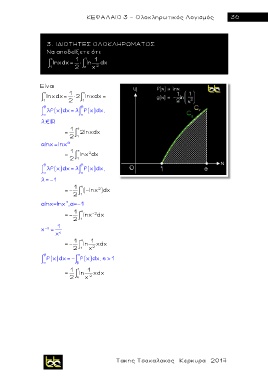
3. ΙΔΙΟΤΗΤΕΣ ΟΛΟΚΛΗΡΩΜΑΤΟΣ
Να αποδείξετε ότι:
e 1 1 1
1 lnx dx= 2 × e ln x 2 dx

Είναι
e 1 e
lnx dx = × 2 lnxdx=
1 2 1
β β
λf(x) dx= λ f(x) dx,
α α
λ
1 e
= 2lnxdx
2 1
αlnx=lnx
1 e
2
= lnx dx
2 1
β β
λf(x) dx= λ f(x) dx,
α α
λ=-1
1 e
=- (-lnx )dx
2
2 1
αlnx =lnx , α= -1
1 e
=- lnx -2 dx
2 1
1
x =
x
1 e 1
=- ln xdx
2 1 x 2
β α
f(x) dx=- f(x) dx , e> 1
α β
1 1 1
= ln xdx
2 e x 2

Τακης Τσακαλακος Κερκυρα 2017