Page 37 - olokliroma

37
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

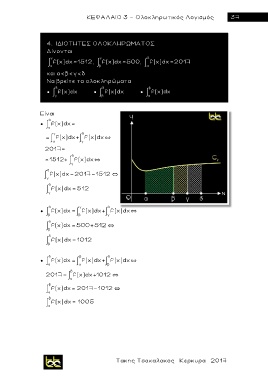
4. ΙΔΙΟΤΗΤΕΣ ΟΛΟΚΛΗΡΩΜΑΤΟΣ
Δίνονται
γ γ δ
α f(x) dx= 1512, β f(x) dx= 500, α f(x) dx= 2017
και α<β<γ<δ
Nα βρείτε τα ολοκληρώματα
δ δ β
● f(x) dx ● f(x) dx ● f(x) dx
γ β α

Είναι

δ
● f(x) dx=
α
γ δ
f(x) dx+ f(x) dx`
α γ
2017=
δ
=1512+ f(x) dx`
γ
δ
f(x) dx 2017 1512 `
γ
δ
f(x) dx= 512
γ

δ γ δ
● f(x) dx f(x) dx+ f(x) dx`
β β γ
δ
f(x) dx=500+512 `
β
δ
f(x) dx= 1012
β

δ β δ
● f(x) dx f(x) dx+ f(x) dx`
α α β
β
2017 f(x) dx+1012 `
α
β
f(x) dx= 2017-1012 `
α
β
f(x) dx= 1005
α

Τακης Τσακαλακος Κερκυρα 2017