Page 39 - olokliroma

39
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

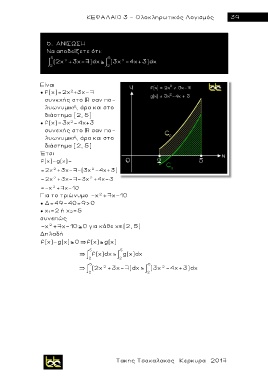
6. ΑΝΙΣΩΣΗ
Nα αποδείξετε ότι:
5 5
2
2 (2x 2 +3x-7) dx 2 (3x - 4x+3) dx

Είναι
● f(x)=2x +3x-7
2
συνεχής στο σαν πο-
λυωνυμική, άρα και στο
διάστημα [2, 5]
● f(x)=3x -4x+3
2
συνεχής στο σαν πο-
λυωνυμική, άρα και στο
διάστημα [2, 5]

Έτσι
f(x)-g(x)=
= 2x 2 +3x-7-(3x - 4x+3)
2
= 2x 2 +3x-7-3x 2 +4x-3
=- x 2 +7x-10
2
Για το τριώνυμο - x +7x-10
● Δ=49-40=9>0
● χ 1=2 ή χ 2=5

συνεπώς
- x +7x-10 0 για κάθε χ (2, 5)
2
Δηλαδή
f(x)-g(x) 0 f(x) g(x)

5 5
f(x) dx g(x) dx
2 2
5 5
2
~ (2x 2 +3x-7) dx (3x - 4x+3) dx
2 2

Τακης Τσακαλακος Κερκυρα 2017