Page 38 - olokliroma

38
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

5. ΠΑΡΑΜΕΤΡΟΣ
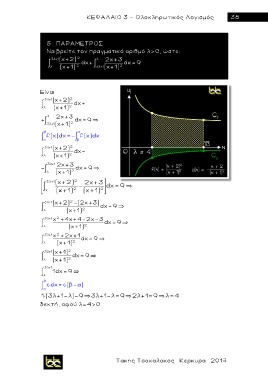
Nα βρείτε τον πραγματικό αριθμό λ>0, ώστε:
3λ+1 (x+2) 2 λ 2x+3
λ (x+1) 2 dx+ 3λ+1 (x+1) 2 dx=9

Είναι

3λ+1 (x+2) 2 dx+
λ (x+1) 2

λ 2x+3
+ dx= 9 ~
3λ+1 (x+1) 2
β α
f(x) dx=- f(x) dx
α β
3λ+1 (x+2) 2 dx-
λ (x+1) 2

3λ+1 2x+3
- dx= 9 ~
λ (x+1) 2

3λ+1 (x+2) 2 - 2x+3 dx= 9 ~
λ (x+1) 2 (x+1) 2

2
3λ+1 (x+2) -(2x+3)
λ (x+1) 2 dx=9 ~
2
3λ+1 x +4x+4-2x-3 dx= 9 ~
λ (x+1) 2
2
3λ+1 x +2x+1 dx= 9 ~
λ (x+1) 2
3λ+1 (x+1) 2 dx=9~
λ (x+1) 2

3λ+1
1 dx= 9 ~
λ
β
c dx= c(β-α)
α
1×(3λ+1-λ)-9~3λ+1-λ=9~2λ+1=9~λ=4
δεκτή, αφού λ=4>0

Τακης Τσακαλακος Κερκυρα 2017