Page 40 - olokliroma

40
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

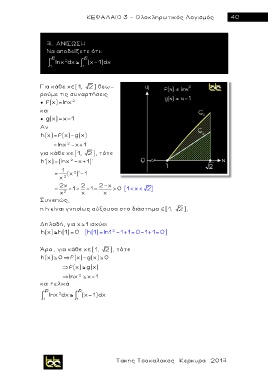
7. ΑΝΙΣΩΣΗ
Nα αποδείξετε ότι:
2 2
2
1 lnx dx 1 (x-1) dx

Για κάθε χ [1, 2] θεω-
ρούμε τις συναρτήσεις
● f(x)=lnx
2
και
● g(x)=x-1
Αν
h(x)= f(x)-g(x)

= lnx -x+1
2
για κάθε χ [1, 2], τότε

h'(x)=(lnx -x+1)'
2
= 1 (x )'-1
2
x 2
2x 2 2-x
= -1= -1= > 0 [1< x< 2 ]

x 2 x x
Συνεπώς,

η h είναι γνησίως αύξουσα στο διάστημα [1, 2],

Δηλαδή, για χ 1 ισχύει
2
h(x) h(1)=0 [h(1)=ln1 -1+1=0-1+1=0 ]

Άρα , για κάθε χ [1, 2], τότε
h(x) 0~ f(x)-g(x) 0

~ f(x) g(x)

~ lnx 2 x-1
και τελικά
2 2
lnx dx (x-1) dx
2
1 1

Τακης Τσακαλακος Κερκυρα 2017