Page 68 - olokliroma

68
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

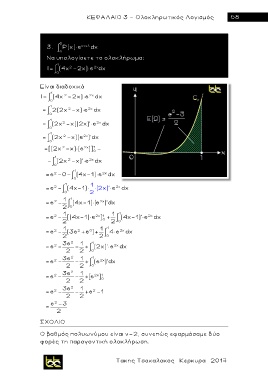
3. β Ρ(x)× e κx+λ dx
α
Να υπολογίσετε το ολοκλήρωμα:
I 1 (4x -2x) e 2x
2
0 dx

Είναι διαδοχικά
1
Ι= (4x -2x) e 2χ dx
2
0
1
2
= 2(2x -x) e 2x dx
0
= 1 (2x -x)(2χ)' e 2x dx
2
0
1
= (2x -x)(e 2x )' dx
2
0
[(2x -x)×(e )] 1 0
2x
2
1
(2x -x)' e dx
2x
2
0
1
e -0 (4x-1) e 2x dx
2
0
1 1
e 2 (4x-1) (2χ)' e 2x dx
0 2
1 1
= e 2 (4x-1) (e )' dx
2x
2 0
1 1 1
= e 2 [(4x-1)× e ] (4x-1)' × e dx
2x 1
2x
2 0 2 0
1 1 1
= e 2 (3e +e ) 4× e 2x dx
2
0
2 2 0
3e 2 1 1
= e 2 (2χ)' × e 2x dx
2 2 0
3e 2 1 1
= e 2 (e 2x )' dx
2 2 0
3e 2 1
= e 2 [e ]
2x 1
2 2 0
3e 2 1
= e 2 e 2 1
2 2
2
e -3
=
2
ΣΧΟΛΙΟ

Ο βαθμός πολυωνύμου είναι ν=2, συνεπώς εφαρμόσαμε δ ύο
φορές τη παραγοντική ολοκλήρωση.

Τακης Τσακαλακος Κερκυρα 2017