Page 73 - olokliroma

73
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

β x
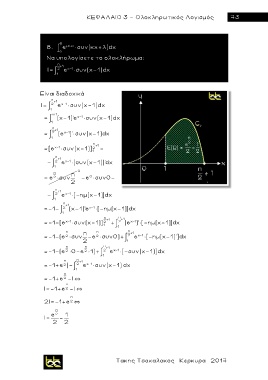
8. α e × συν(κx+λ) dx
Να υπολογίσετε το ολοκλήρωμα:
π +1
I 1 2 e x 1 × συν(x-1) dx

Είναι διαδοχικά
π +1
I= 2 e x-1 × συν(x-1) dx
1
π+1
= (x-1)'e x -1 × συν(x-1) dx
1
π +1
= 2 (e x -1 )' × συν(x-1) dx
1
π +1
=[e x -1 × συν(x-1) ] 2 -
1
π +1
- 2 e x -1 ×(συν(x-1) )'dx
1
0
π π
= e × συν -e × συν0-
0
2
2
π +1
- 2 e x -1 ×[-ημ(x-1) ] dx
1
π +1
=-1- 2 (χ-1)'e x -1 ×[-ημ(x-1) ] dx
1
π +1 π +1
=-1-[e x -1 × συν(x-1) ] 2 2 (e x -1 )' ×[-ημ(x-1) ] dx
1
1
π π π π +1
=-1-(e × συν -e × συν0) 2 e x-1 ×[-ημ(x-1) '] dx
2
2
2 1
π π π +1
=-1-(e × 0-e × 1) 2 e x -1 ×[-συν(x-1) ] dx
2
2
1
π π +1
=-1+e ) 2 e x -1 × συν(x-1) dx
2
1
π
=-1+e 2 `
π
=-1+e 2 `
π
2Ι=-1+e `
2
π
e 2 1
Ι= -
2 2

Τακης Τσακαλακος Κερκυρα 2017