Page 75 - olokliroma

75
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

10. ΘΕΩΡΗΤΙΚΗ
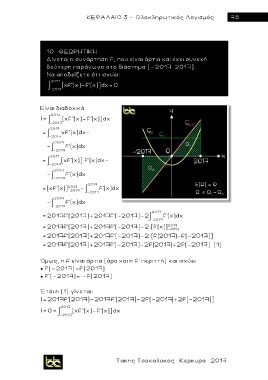
Δίνεται η συνάρτηση f, που είναι άρτια και έχει συνεχή
δεύτερη παράγωγο στο διάστημα [-2017, 2017].
Να αποδείξετε ότι ισχύει:
2017
-2017 [χf''(x)-f'(x)] dx= 0

Είναι διαδοχικά
2017
I= [χf''(x)-f'(x)] dx
-2017
2017
= χf''(x)dx -
-2017
2017
- f'(x)dx
-2017
2017
= [χf'(x)] f'(x)dx -
-2017
- 2017 f'(x)dx
-2017
2017
=[χf'(x) ] 2017 - f'(x)dx -
-2017
-2017
2017
- f'(x)dx
-2017
2017
= 2017f'(2017)+2017f'(-2017) -2 f'(x)dx
-2017
=2017f'(2017)+2017f'(-2017) -2 [f(x) ] 2017
-2017
=2017f'(2017)+2017f'(-2017) -2 [f( 2017 ) -f(-2017)]

=2017f'(2017)+2017f'(-2017) -2f( 2017 ) +2f(-2017) (1)

Όμως, η f είναι άρτια (άρα και η f' περιττή) και ισχύει
● f(-2017)=f(2017)

● f'(-2017)= -f(2017)

Έτσι η (1) γίνεται:
Ι=2017f'(2017)-2017f'(2017) -2f(-2017 ) +2f(-2017)]
2017
I= 0= [χf''(x)-f'(x)] dx
-2017

Τακης Τσακαλακος Κερκυρα 2017