Page 87 - olokliroma

87
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

9. ΑΝΤΙΚΑΤΑΣΤΑΣΗ (ΘΕΩΡΗΤΙΚΗ)
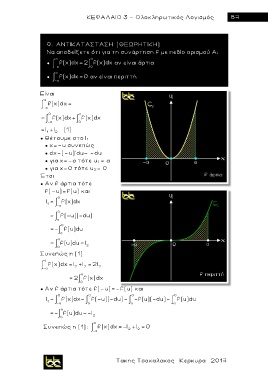
Να αποδείξετε ότι για τη συνάρτηση f με πεδίο ορισμού Α:

● -α f(x) dx 2 0 f(x) dx αν είναι άρτια

● -α f(x) dx 0 αν είναι περιττή

Είναι

f(x) dx
-α
0
f(x) dx f(x) dx
-α 0
= Ι Ι (1)
1 2
● Θέτουμε στο Ι 1
● x=-u συνεπώς
● dx=(-u)'du= -du

● για χ=-α τότε u 1 = α
● για χ=0 τότε u 2= 0
Έτσι
● Αν f άρτια τότε
f(-u)=f(u) και
0
Ι = f(x)dx
1
-α
0
= f(-u)(-du)
α
0
=- f(u)du
α
= α f(u)du I
0 2
Συνεπώς η (1)

α
f(x) dx Ι Ι = 2Ι
-α 2 2 2
α
= 2 f(x) dx
0
● Αν f άρτια τότε f(-u)=-f(u) και
0 0 0 0
Ι = f(x)dx = f(-u)(-du) -f(u)(-du)= f(u)du
1
-α α α α
=- α f(u)du - I
0 2
α
Συνεπώς η (1): f(x) dx Ι Ι = 0
-α 2 2

Τακης Τσακαλακος Κερκυρα 2017