Page 88 - olokliroma

88
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

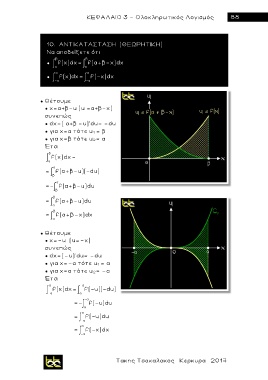
10. ΑΝΤΙΚΑΤΑΣΤΑΣΗ (ΘΕΩΡΗΤΙΚΗ)
Να αποδείξετε ότι

● α f(x) dx α f(α+β-x) dx

● -α f(x) dx -α f(-x) dx

● Θέτουμε
● x=α+β-u (u =α+β-χ )
συνεπώς
● dx=( α+β -u)'du= -du
● για χ=α τότε u 1 = β

● για χ=β τότε u 2= α
Έτσι
β
f(x) dx =
α
α
= f(α+β-u) (-du)
β

=- α f(α+β-u) du
β
β
= f(α+β-u) du
α
β
= f(α+β-χ) dχ
α

● Θέτουμε
● x=-u (u=-χ )
συνεπώς
● dx=(-u)'du= -du
● για χ=-α τότε u 1 = α
● για χ=α τότε u 2= -α
Έτσι

f(x) dx f(-u) (-du)
-α α
f(-u) du
α

f(-u) du
-α
α
f(-x) dx
-α

Τακης Τσακαλακος Κερκυρα 2017