Page 89 - olokliroma

89
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

11. ΑΝΤΙΚΑΤΑΣΤΑΣΗ (ΕΦΑΡΜΟΓΗ)
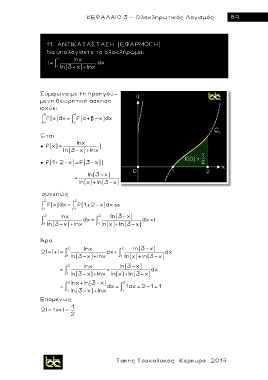
Να υπολογίσετε το ολοκλήρωμα:
2 lnx
1 ln(3-x)+lnx dx

Σύμφωνα με τη προηγού-
μενη θεωρητική άσκηση
ισχύει
β β
f(x) dx= f(α+β-x) dx
α α

Έτσι
lnx
● f(x) )
ln(3-x)+lnx

● f(1+2-x) f(3-x))

ln(3-x)

ln(x)+ln(3-x)

συνεπώς
2 2
f(x) dx= f(1+2-x) dx`
1 1
2 lnx dx= 2 ln(3-x)
1 ln(3-x)+lnx 1 ln(x)+ln(3-x) dx=I

Άρα
2 lnx 2 ln(3-x)
2 Ι= Ι+Ι= dx+ dx
1 ln(3-x)+lnx 1 ln(x)+ln(3-x)

2 lnx ln(3-x)
= + dx
1 ln(3-x)+lnx ln(x)+ln(3-x)

2 lnx+ln(3-x) 2
= dx 1 dx 2 1 1
1 ln(3-x)+lnx 1
Επομένως
1
2 Ι= 1` Ι =
2

Τακης Τσακαλακος Κερκυρα 2017