Page 73 - Buku Aljabar Linear & Matriks

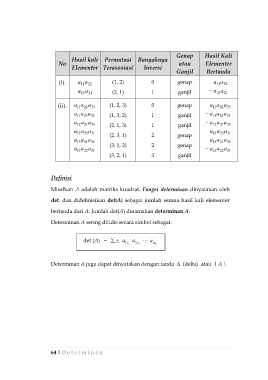
Genap Hasil Kali
Hasil kali Permutasi Banyaknya
No atau Elementer
Elementer Terasosiasi Inversi
Ganjil Bertanda

(i). a 11 a 22 (1, 2) 0 genap a 11 a 22
a 12 a 21 (2, 1) 1 ganjil − a 12 a 21

(ii). a 11 a 22 a 33 (1, 2, 3) 0 genap a 11 a 22 a 33
a 11 a 23 a 32 (1, 3, 2) 1 ganjil − a 11 a 23 a 32

a 12 a 21 a 33 (2, 1, 3) 1 ganjil − a 12 a 21 a 33
a 12 a 23 a 31 a 12 a 23 a 31

a 13 a 21 a 32 (2, 3, 1) 2 genap a 13 a 21 a 32
a 13 a 22 a 31 (3, 1, 2) 2 genap − a 13 a 22 a 31
(3, 2, 1) 3 ganjil

Definisi

Misalkan A adalah matriks kuadrat. Fungsi determinan dinyatakan oleh

det, dan didefinisikan det(A) sebagai jumlah semua hasil kali elementer

bertanda dari A. Jumlah det(A) dinamakan determinan A.

Determinan A sering ditulis secara simbol sebagai:

det (A) =   a a 2 j 2  a nj n
1
j 1

Determinan A juga dapat dinyatakan dengan tanda  (delta) atau | A |.

64 | D e t e r m i n a n