Page 43 - Matematika Integral

Tugas Mandiri tak terstruktur 12

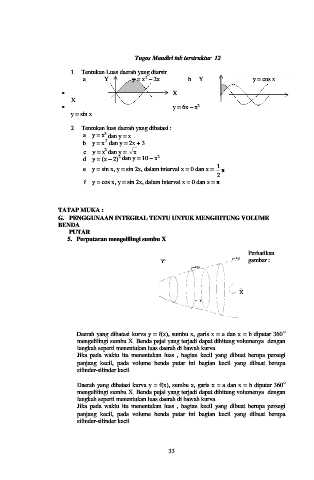
1. Tentukan Luas daerah yang diarsir.
2
a. Y y = x – 2x b. Y y = cos x

 X
X
2
 y = 6x – x
y = sin x

2. Tentukan luas daerah yang dibatasi :
3
a. y = x dan y = x
2
b. y = x dan y = 2x + 3
2
c. y = x dan y = x
2
2
d. y = (x – 2) dan y = 10 – x
1
e. y = sin x, y = sin 2x, dalam interval x = 0 dan x = π
2
f. y = cos x, y = sin 2x, dalam interval x = 0 dan x = π

TATAP MUKA :
G. PENGGUNAAN INTEGRAL TENTU UNTUK MENGHITUNG VOLUME
BENDA
PUTAR
5. Perputaran mengelilingi sumbu X

Perhatikan
y = f (x) gambar :
Y
y = f (x)

X

x

o
Daerah yang dibatasi kurva y = f(x), sumbu x, garis x = a dan x = b diputar 360
mengelilingi sumbu X. Benda pejal yang terjadi dapat dihitung volumenya dengan
langkah seperti menentukan luas daerah di bawah kurva..
Jika pada waktu itu menentukan luas , bagian kecil yang dibuat berupa persegi
panjang kecil, pada volume benda putar ini bagian kecil yang dibuat berupa
silinder-silinder kecil.

o
Daerah yang dibatasi kurva y = f(x), sumbu x, garis x = a dan x = b diputar 360
mengelilingi sumbu X. Benda pejal yang terjadi dapat dihitung volumenya dengan
langkah seperti menentukan luas daerah di bawah kurva..
Jika pada waktu itu menentukan luas , bagian kecil yang dibuat berupa persegi
panjang kecil, pada volume benda putar ini bagian kecil yang dibuat berupa
silinder-silinder kecil.

33